The Mathematics and Categories of Starting Hands in Texas Hold’em

Poker strategy begins before the first community card is even dealt. In Texas Hold’em, the two private hole cards each player receives dictate the range of possibilities for how they can proceed in the hand. Understanding the math behind how many starting hands exist, and how they can be categorized, is a cornerstone of building strong preflop strategy.

1. How Many Starting Hands Exist?

Texas Hold’em is played with a standard 52-card deck. Each player is dealt two hole cards. To calculate the number of possible starting hands, we simply count the number of two-card combinations: $${52 \choose 2} = \frac{52 \times 51}{2} = 1326$$

So there are 1,326 distinct starting hand combinations.

However, many of these are strategically equivalent. For example, ♠A♥K is strategically the same as ♦A♣K if suits aren’t relevant. To simplify, we group them into broader categories.

Step 2: Distinguishing Equivalent Hands

Not all of these 1,326 are strategically unique. For example, ♦A♣K is strategically the same as ♠A♥K — they are both Ace-King offsuit. Therefore, we group them into hand classes.

Pairs: 13 possible ranks (AA, KK, …, 22). Each pair can be made in 6 ways (e.g., A♠A♥, A♠A♦, etc.).
- Total combinations: $13 \times 6 = 78$
Suited non-pairs: Pick 2 different ranks, then same suit. There are ${13 \choose 2} = 78$ unique rank combinations, and each can occur in 4 suits.
- Total combinations: $78 \times 4 = 312$
Offsuit non-pairs: Again 78 rank combinations, but now the suits differ. For each rank combo, there are 16 total suit combinations minus the 4 suited ones = 12 offsuit versions.
- Total combinations: $78 \times 12 = 936$

Adding them up: $$78 + 312 + 936 = 1326$$

So the count matches perfectly.

Step 3: Hand Categories

To make sense of these, poker players group hands into 169 distinct categories:

13 pairs (AA down to 22)
78 suited hands (e.g., AKs, AQs, JTs, 54s, etc.)
78 offsuit hands (e.g., AKo, QJo, 97o, etc.)

That’s: $$13 + 78 + 78 = 169$$

These 169 categories are usually represented in a 13×13 matrix:

Diagonal: Pairs (AA down to 22)
Above diagonal: Suited hands (AKs, QJs, etc.)
Below diagonal: Offsuit hands (AKo, JTo, etc.)

This grid makes it easy to visualize and group hands into broader strategy categories.

(See Table 1, with colors: red = pairs, blue = suited, green = offsuit. Premium hands are outlined in gold, strong hands in orange.)

4. Strategic Groupings of Starting Hands

While the 169 categories are exact, players usually think in broader strategic buckets that guide preflop decisions.

4.1 Premium Hands

Examples: AA, KK, QQ, AKs
Traits: These are the strongest holdings in poker. They dominate most other hands and are usually played aggressively (raising, re-raising, and rarely folded).
Frequency: Premium hands appear very rarely — less than 2% of the time.

4.2 Strong Hands

Examples: JJ, TT, 99, AQs, AKo
Traits: Very strong but slightly more vulnerable than premiums. They can dominate weaker hands but must be played carefully against aggression.
Strategy: Often raised preflop, but sometimes just called in cautious spots.

4.3 Speculative Hands

Examples: Small pairs (22–88), suited connectors (76s, JTs), suited one-gappers (T8s, 97s), suited aces (A2s–A9s).
Traits: These hands play well in multiway pots because they can hit disguised strong hands (straights, flushes, sets).
Strategy: Good for calling raises in position but dangerous when played too loosely.

4.4 Weak Hands (Trash)

Examples: Offsuit, unconnected low cards (92o, J4o, 72o).
Traits: Rarely win without significant luck. Easily dominated and tough to play profitably.
Strategy: Almost always folded preflop, especially in full-ring games.

5. Why This Breakdown Matters

Mathematical grounding: Knowing there are 1,326 combinations but only 169 categories helps simplify poker theory.
Equity considerations: Premium hands have high equity against random hands, while speculative hands rely on implied odds.
Range construction: Players use the starting hand chart to build balanced ranges (deciding what to raise, call, or fold in different positions).
Strategic awareness: Recognizing hand strength categories prevents beginners from overplaying weak holdings.

7. Probability of Being Dealt Specific Starting Hands

Since there are 1,326 total possible combinations, the probability of being dealt a particular type of hand depends on how many combinations exist for it.

7.1 Any Specific Pocket Pair

Example: AA
Number of combinations: 6
Probability:

$$\frac{6}{1326} \approx 0.45\% \quad \text{(about 1 in 221 hands)}$$

This is the same for every pair (KK, QQ, …, 22).

7.2 Any Pocket Pair (All 13)

Number of combinations: 78
Probability:

$$\frac{78}{1326} \approx 5.9\% \quad \text{(about 1 in 17 hands)}$$

So on average, you’ll be dealt a pair once every couple of orbits.

7.3 Specific Suited Hand

Example: AKs
Number of combinations: 4 (♠A♠K, ♥A♥K, etc.)
Probability:

$$\frac{4}{1326} \approx 0.30\% \quad \text{(about 1 in 331 hands)}$$

7.4 Any Suited Hand (All ranks combined)

Number of combinations: 312
Probability:

$$\frac{312}{1326} \approx 23.5\% \quad \text{(about 1 in 4 hands)}$$

So roughly one out of every four starting hands is suited.

7.5 Specific Offsuit Hand

Example: AKo
Number of combinations: 12
Probability:

$$\frac{12}{1326} \approx 0.90\% \quad \text{(about 1 in 110 hands)}$$

7.6 Any Ace

If you want to know the probability of being dealt at least one Ace:

Total hands without an Ace = choose both cards from the other 48 cards:

$${48 \choose 2} = 1128$$

Probability of no Ace:

$$\frac{1128}{1326} \approx 85.1\%$$

Therefore, probability of at least one Ace:

$$1 – 0.851 \approx 14.9\%$$

So you’ll see an Ace about once every 7 hands.

7.7 Premium Hands as a Group

Premium hands are often defined as AA, KK, QQ, AKs.

Total combinations = 6 + 6 + 6 + 4 = 22
Probability:

$$\frac{22}{1326} \approx 1.7\% \quad \text{(about 1 in 59 hands)}$$

This explains why big pocket pairs feel so rare — they are!

7.8 Any Two Cards Connected (for straights)

Example: JT, 76, 54, etc.
There are 12 rank sequences possible (AK down to 32). Each has 16 offsuit + 4 suited = 20 combinations.
Total = $12 \times 20 = 240$
Probability:

$$\frac{240}{1326} \approx 18.1\%$$

So about 1 in 5 hands is some form of connector.

8. Starting Hand Chart

Here’s the probability-annotated starting hand chart:

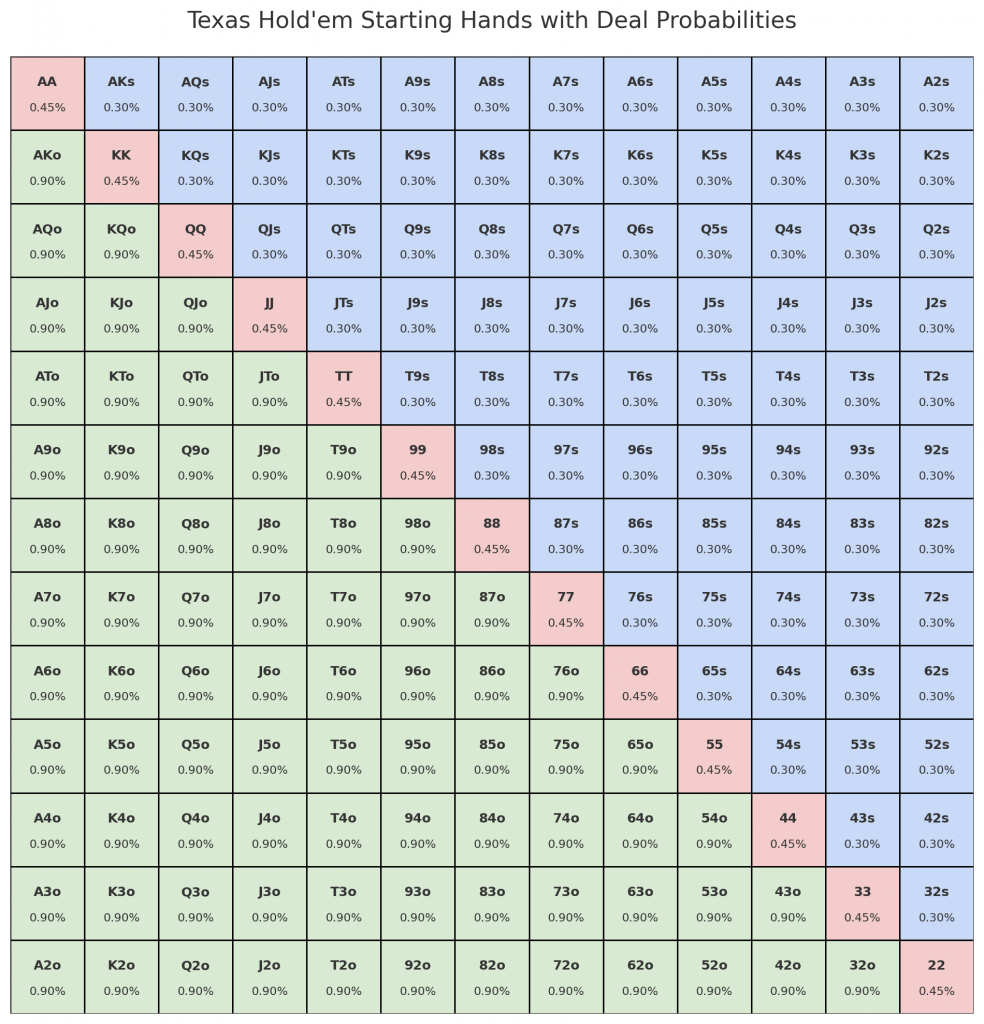
Each cell shows the hand name and the chance of being dealt that exact category.
Pairs (AA, KK, …, 22) each ≈ 0.45%
Suited hands (AKs, QJs, …) each ≈ 0.30%
Offsuit hands (AKo, JTo, …) each ≈ 0.90%

This visualization makes it clear how rare premium hands really are, and why most of poker is about playing less-than-ideal hands well.

9. Why Probabilities Matter

Expectation: Knowing how rare a premium hand is prevents players from waiting endlessly for “monsters.”
Balance: Helps construct ranges (you can’t always have AA; most of the time, your range is weaker).
Strategic discipline: Shows why folding is normal — most hands are weak and not worth playing.

Final Takeaway

There are 1,326 total starting hands in Texas Hold’em.
They collapse into 169 categories (13 pairs, 78 suited, 78 offsuit).
Probabilities reveal how often you’ll see each type:
- AA: once every 221 hands
- Any pocket pair: once every 17 hands
- Suited cards: once every 4 hands
- Premiums: once every 59 hands

Poker is a game of rarity, patience, and timing. The math of starting hands provides the foundation for understanding not just what you hold, but how often you should expect to hold it — and that’s essential to developing a winning mindset.