The Paradox of Human Intuition: Probability, Evolution, and Online Poker

Human cognition exhibits a paradox: while we are adept at estimating magnitudes such as distance, weight, and duration—abilities honed by natural selection in ancestral environments—we are systematically poor at judging probabilities. This evolutionary asymmetry arises because survival pressures reinforced perceptual accuracy in continuous variables but did not cultivate abstract probabilistic reasoning. The result is a suite of well-documented biases, including the gambler’s fallacy, neglect of base rates, and overconfidence. Online poker provides a natural laboratory to examine this mismatch, as it places humans in a controlled probabilistic environment where outcomes can be precisely calculated but intuition frequently misleads. This article reviews evidence from evolutionary psychology and cognitive science, illustrates probabilistic misconceptions with poker examples, and discusses corrective strategies through probabilistic literacy, computational tools, and game theory. The case of online poker underscores the broader importance of understanding human limitations in probabilistic reasoning in domains such as finance, medicine, and policy-making.
1. Introduction

Probability is a cornerstone of modern decision science, yet humans routinely fail to reason about it correctly. From misjudging the likelihood of rare events (Slovic et al., 1979) to succumbing to gambling fallacies (Tversky & Kahneman, 1971), our probabilistic errors have real-world consequences.
In contrast, our species demonstrates impressive proficiency in estimating physical magnitudes. A forager could reliably judge the distance to a fruit tree, the time until nightfall, or the load a branch could bear. These skills emerge spontaneously without formal training and remain robust across cultures.
This divergence reflects evolutionary pressures. Estimating distances, weights, and durations had immediate fitness consequences, while calculating probabilities did not. Consequently, probabilistic reasoning is a domain of evolutionary “mismatch”—an area where modern environments demand skills our brains were not optimized to perform (Li et al., 2018).
Online poker highlights this mismatch. It is a game in which success depends on probabilistic reasoning, yet human players often default to heuristics and biases. At the same time, poker illustrates how technology and formal models can augment human cognition, offering insights into broader strategies for overcoming probabilistic limitations.
2. Evolutionary Adaptations for Magnitude Estimation
Humans exhibit near-universal competence in estimating continuous variables. This competence can be explained through:
- Distance estimation: Throwing accuracy in spear-hunting or rock-throwing relies on precise judgments of distance and trajectory (Foley, 1987). Visual and vestibular systems provide rich feedback, supporting reliable estimation.
- Weight estimation: Judging how much force is needed to carry or lift an object minimizes injury and energy waste. Even children show strong intuitive weight discrimination (Chapanis & Lindenbaum, 1959).
- Temporal estimation: Time perception underpins survival tasks such as evading predators, coordinating social activity, and anticipating environmental changes (Block, 1990).
Empirical studies suggest humans estimate continuous magnitudes with relatively low error compared to probability. For example, Stevens (1957) demonstrated psychophysical scaling that, while nonlinear, is systematic and predictable. By contrast, probability judgments tend to be inconsistent and prone to distortion (Kahneman & Tversky, 1979).
3. The Evolutionary Blind Spot in Probability Estimation

Unlike magnitudes, probabilities are not directly observable. They require abstraction: the recognition of frequencies across repeated events and the ability to generalize from them. Evolutionary psychology suggests our ancestors rarely encountered environments that rewarded precise probability calculation (Cosmides & Tooby, 1996). Instead, they relied on heuristics—cognitive shortcuts that were sufficient for survival but misfire in modern contexts.
Key biases include:
- Gambler’s fallacy: Misinterpreting independence, such as believing a fair coin is “due” for heads after several tails (Tversky & Kahneman, 1971).
- Overconfidence: Inflated certainty in one’s judgments, linked to evolutionary advantages in dominance contests but maladaptive in probabilistic games (Johnson & Fowler, 2011).
- Neglect of base rates: Focusing on salient case details rather than statistical priors (Bar-Hillel, 1980).
- Illusion of control: Attributing outcomes to skill in fundamentally stochastic settings (Langer, 1975).
These biases persist even among educated populations, underscoring the robustness of the evolutionary mismatch.
4. Online Poker as a Natural Laboratory

Poker provides a controlled environment where probability is central and outcomes can be precisely modeled. Unlike real-world risks (e.g., weather, health), poker probabilities are well-defined and quantifiable, making it an ideal domain to examine human miscalibration.
4.1. Probability calculations in poker
At its core, poker is a game of incomplete information governed by probability. Examples include:
- Drawing to a flush: After the flop (three cards), a player with two suited cards has 9 “outs” (remaining cards of that suit). The probability of hitting the flush by the river is approximately 35% (1 – ((38/47) × (37/46))).
- Pocket aces pre-flop: The strongest starting hand in Texas Hold’em, yet it only wins against a random hand about 85% of the time. Novice players frequently overestimate this probability as near-certain.
- Set mining with pocket pairs: The chance of flopping a set (three of a kind) with a pocket pair is about 12%. Players often chase this event without accounting for implied pot odds.
These examples highlight the gap between mathematical reality and human intuition.
4.2. Pattern-seeking in randomness
Players perceive “hot” and “cold” streaks, despite each hand being independent. This reflects humans’ adaptive but overgeneralized tendency to detect patterns in noise (Shermer, 2008).
4.3. Tilt and emotional interference
Poker variance (short-term randomness) often triggers tilt, where players abandon probabilistic strategies due to frustration. This illustrates how emotion exacerbates cognitive bias, overriding rational models of probability.
4.4. Corrective tools in online environments

Unlike live poker, online platforms allow players to deploy statistical aids:
- Heads-up displays (HUDs) provide frequency data on opponents’ behaviors.
- Equity calculators allow precise hand-comparison simulations.
- Poker Mining and hand histories by hhDealer lead to statistical evidence instead of empirical feelings.
These tools function as cognitive scaffolds, compensating for the evolutionary blind spot. Skilled players integrate them to align decisions with probability theory, gaining a structural advantage over intuition-driven opponents.
5. Broader Implications: Probability Beyond Poker
The lessons of poker extend to other domains where humans confront probabilistic environments:
- Finance: Investors misjudge risk-return trade-offs, leading to bubbles and crashes (Shiller, 2000).
- Medicine: Patients and even physicians neglect base rates when interpreting diagnostic tests (Gigerenzer et al., 2007).
- Policy: Public misperceptions of rare risks (e.g., plane crashes vs. car accidents) influence policy disproportionally (Slovic, 1987).
Poker thus serves as a microcosm of the broader human struggle with probability.
6. Figures and Tables
Figure 1: Comparison of human accuracy in estimating magnitudes (distance, weight) vs. probabilities (graph of average error rates from experimental studies).
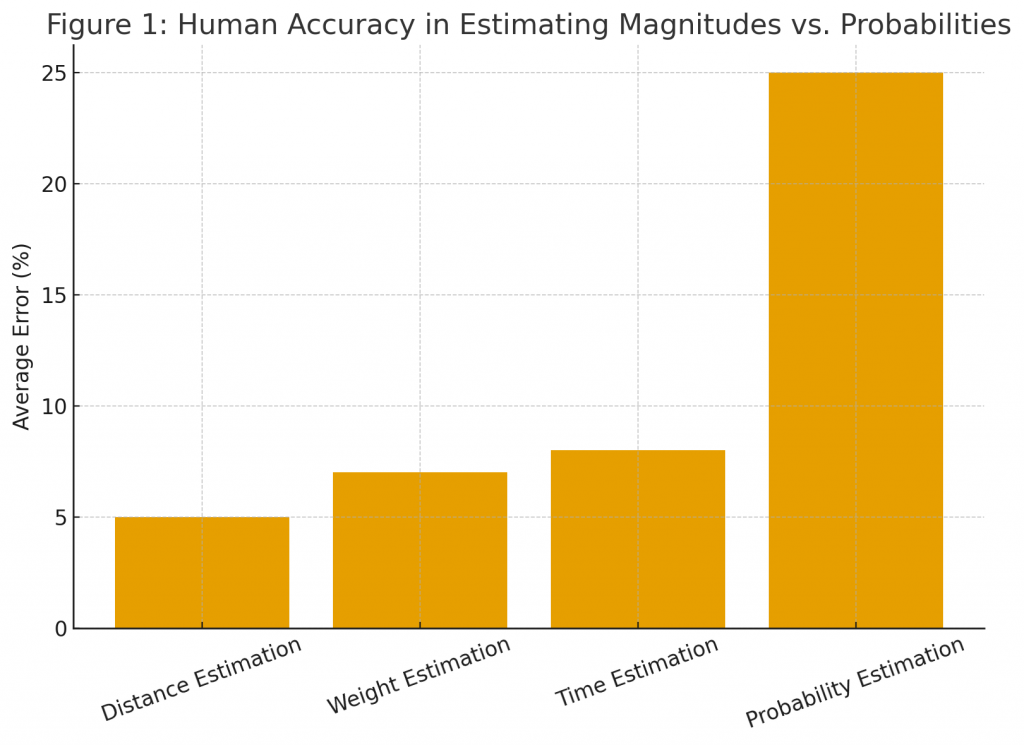
Figure 2: Probability of common poker outcomes (flush, set, pocket aces winning) contrasted with average player estimations (bar chart).
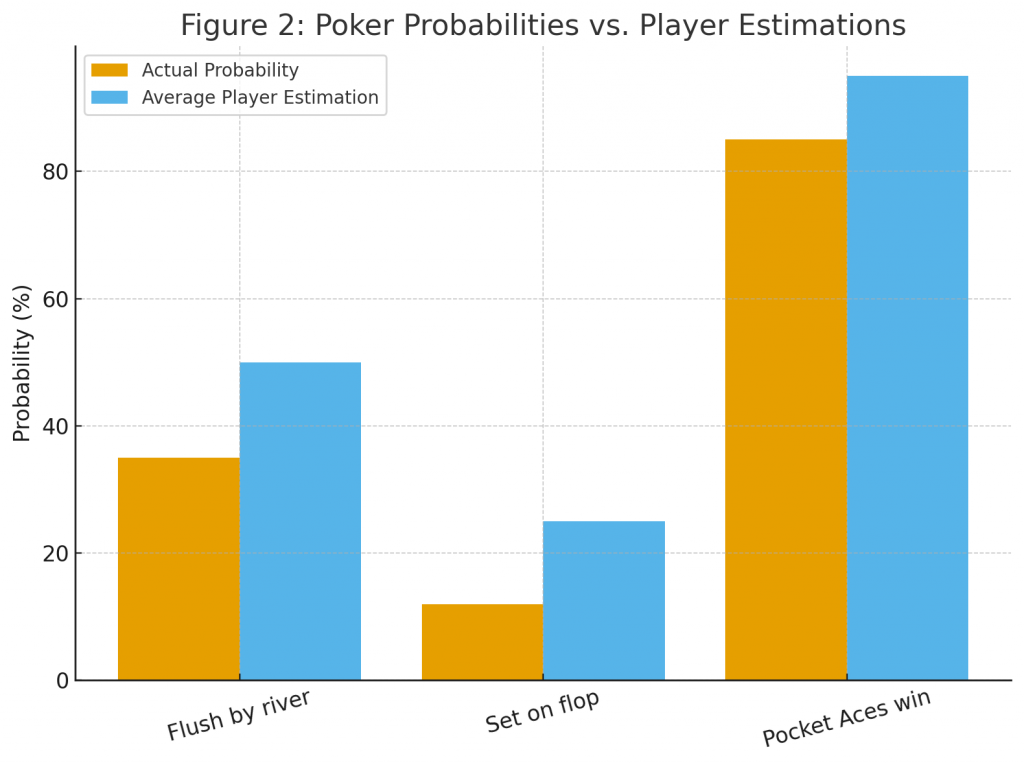
Table 1: Cognitive Biases Relevant to Probability and Poker
| Bias | Evolutionary Root | Manifestation in Poker |
|---|---|---|
| Gambler’s fallacy | Pattern detection in stochastic environments | Believing a losing streak means a win is “due” |
| Overconfidence | Fitness advantage in dominance contests | Overestimating skill or hand strength |
| Neglect of base rates | Preference for salient over statistical cues | Ignoring statistical odds when making calls |
| Illusion of control | Attributing agency to random outcomes | Thinking betting patterns influence random deals |
| Hot-hand fallacy | Overgeneralization of success streaks in ancestral hunting/fighting | Assuming recent wins mean a player is “hot” and more likely to continue winning |
| Availability heuristic | Reliance on easily recalled events | Overestimating the frequency of bad beats because they are vivid and memorable |
| Confirmation bias | Tendency to seek evidence supporting prior beliefs | Remembering times when “luck” seemed to be against them, while ignoring counterexamples |
| Anchoring bias | Reliance on initial values for decision-making | Fixating on an opponent’s first bet size and misjudging later probabilities |
| Outcome bias | Judging decision quality by result rather than process | Assuming a poor call was “correct” if it happened to win due to luck |
| Sunk-cost fallacy | Avoiding loss of prior investments | Continuing to play a weak hand because of chips already invested |
| Risk compensation | Adjusting risk-taking based on perceived safety | Playing more recklessly online because variance feels “less real” without physical chips |
| Survivorship bias | Learning from observed “winners” while ignoring failures | Copying aggressive strategies from famous players while neglecting failed imitators |
| Regression to the mean neglect | Misinterpreting natural variance as meaningful | Assuming a downswing reflects declining skill rather than statistical fluctuation |
7. Conclusion
Human cognition evolved to estimate magnitudes directly tied to survival but not abstract probabilities. This evolutionary gap manifests in systematic probabilistic errors, vividly demonstrated in online poker. Yet poker also illustrates pathways for overcoming these biases: formal education in probability, adoption of computational aids, and application of game-theoretic reasoning.
As the modern world increasingly demands probabilistic literacy—whether in navigating financial markets, medical risks, or climate predictions—the lessons from poker are clear. Recognizing the limits of human intuition is the first step; building cultural and technological scaffolds to support probabilistic reasoning is the second.
References
- Bar-Hillel, M. (1980). The base-rate fallacy in probability judgments. Acta Psychologica, 44(3), 211–233.
- Block, R. A. (1990). Cognitive models of psychological time. Psychology Press.
- Chapanis, A., & Lindenbaum, L. (1959). A quantitative relationship between perceived and actual weights. Science, 129(3359), 111–112.
- Cosmides, L., & Tooby, J. (1996). Are humans good intuitive statisticians after all? Rethinking some conclusions from the literature on judgment under uncertainty. Cognition, 58(1), 1–73.
- Foley, R. (1987). Another unique species: Patterns in human evolutionary ecology. Longman Scientific.
- Gigerenzer, G., Gaissmaier, W., Kurz-Milcke, E., Schwartz, L. M., & Woloshin, S. (2007). Helping doctors and patients make sense of health statistics. Psychological Science in the Public Interest, 8(2), 53–96.
- Johnson, D. D. P., & Fowler, J. H. (2011). The evolution of overconfidence. Nature, 477(7364), 317–320.
- Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263–291.
- Langer, E. J. (1975). The illusion of control. Journal of Personality and Social Psychology, 32(2), 311–328.
- Li, N. P., van Vugt, M., & Colarelli, S. M. (2018). The evolutionary mismatch hypothesis: Implications for psychological science. Current Directions in Psychological Science, 27(1), 38–44.
- Shermer, M. (2008). The Believing Brain. Times Books.
- Shiller, R. J. (2000). Irrational exuberance. Princeton University Press.
- Slovic, P. (1987). Perception of risk. Science, 236(4799), 280–285.
- Slovic, P., Fischhoff, B., & Lichtenstein, S. (1979). Rating the risks. Environment: Science and Policy for Sustainable Development, 21(3), 14–39.
- Stevens, S. S. (1957). On the psychophysical law. Psychological Review, 64(3), 153–181.
- Tversky, A., & Kahneman, D. (1971). Belief in the law of small numbers. Psychological Bulletin, 76(2), 105–110.